29日のエントリには、ひさまつさんから必読文献という言葉を頂いた。少し遅くなったが、改めて感謝。
一昨日はガイトナー案に関し3種類の分布について数値シミュレーションをしてみたが、その際、α(自己資金比率)はガイトナー案の1/7(≒0.143)固定とした。今日は、αを変化させた場合の各変数の動きを見てみる。
一様分布
P〜U[0,200]の一様分布で、αを0から1まで0.05刻みに変更した場合。
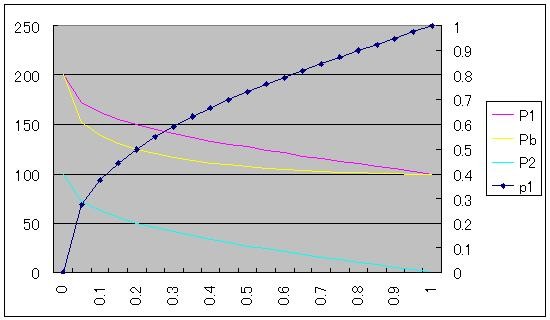
Pの期待値E[P]は上限の半分なので常に100となる(グラフでは省略)。
30日エントリで議論したように、α=0(⇒p1=1)とα=1(⇒p1=0)はモデルの範囲外となるが、ここでは極限値として求めた。
αが上昇すれば、ブレーク・イーブン買取価格PbのE[P]に対するプレミアムは減少していく。
正規分布
次に、P〜N[100,50]の正規分布で、αを0.13から0.43まで0.02刻みに変更した場合。
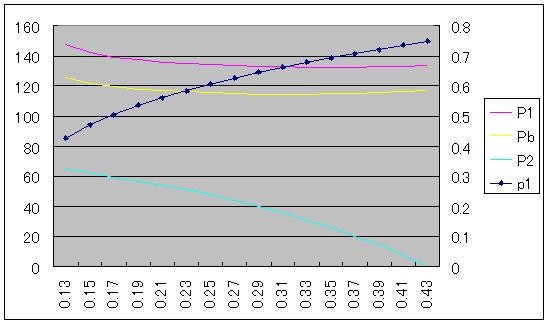
αが0.1近くまで下がると解が求められなくなること、および、αが0.45以上ではP2がマイナスになる(∵通常の正規分布なので下限は無い)ことから、αを上記の範囲とした。
PbのE[P]に対するプレミアムは、この範囲内では25.6%(α=0.13)→16.6%(α=0.43)と10%足らずの低下に留まる(αが一定値(〜0.31)を超えると、むしろ増加傾向が見られる。詳しくは本エントリの末尾参照)。
対数正規分布
最後に、ln(P)〜N[ln(100)-0.5^2/2(≒4.48) , 0.5]の対数正規分布で、αを0.05から0.95まで0.05刻みに変更した場合(前回同様、Pの期待値が100になるようにしてある)。

正規分布の場合と異なり、αを0.15から0.45まで増やすと、PbのE[P]に対するプレミアムは22.0%から2.3%と大きく減少する。ちなみに一様分布の場合の同区間のプレミアム変化は31.0%から9.0%なので、この変化幅に着目した場合、対数正規分布から得られる結果は正規分布よりもむしろ一様分布に近い。
このシミュレーション結果からすると、ノンリコースローン比率をせいぜい5〜6割に留めておけば、プレミアムは5%以下とそれほど大きくならないことが分かる。ガイトナー案のように同比率を6/7まで増やしてしまうと、その大きさは2割を超え、無視できないものとなる。
あるいはひょっとすると、ガイトナー案では、こうした数値シミュレーションにより、目標とするプレミアムから逆算してノンリコースローン比率を決めたのかもしれない。クルーグマンはこれは銀行への事実上の補助金と批判したが、そう考えると、むしろその補助金こそがそもそもの目的であり、高いノンリコースローン比率はその目標値から付随的に決まったに過ぎないことになる。
<おまけ>
正規分布でαを0.93まで延長した場合。
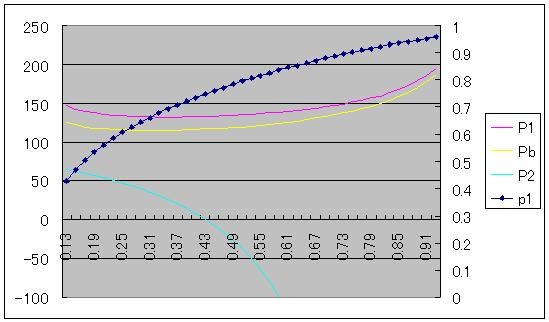
前述の通り、αが一定値(〜0.31)を超えると、P1、Pbはむしろαと共に増加してしまい、αが1に近づくにつれその増加傾向が明確になる。
一様分布や対数正規分布のようにP2に0という下限制約があれば、P2がその下限に近づくにつれ、P1、Pb共に100に漸近することになる。それに対し、正規分布ではその下限が無く、P2がαの増大に伴いマイナス方向にいくらでも伸びていく一方で、確率p1には1という上限があるため、p1P1+(1-p1)P2=100の条件のもとではP1が増加せざるを得ないわけだ。
従って、今回のシミュレーションに関しては正規分布は基本的に不適であることが分かる。