というNBER論文が上がっている(2年前のWP)。原題は「Bank Risk Dynamics and Distance to Default」で、著者はStefan Nagel(シカゴ大)、Amiyatosh Purnanandam(ミシガン大)。
以下はその要旨。
We adapt structural models of default risk to take into account the special nature of bank assets. The usual assumption of log-normally distributed asset values is not appropriate for banks. Typical bank assets are risky debt claims, which implies that they embed a short put option on the borrowers’ assets, leading to a concave payoff. This has important consequences for banks’ risk dynamics and distance to default estimation. Due to the payoff non-linearity, bank asset volatility rises following negative shocks to borrower asset values. As a result, standard structural models in which the asset volatility is assumed to be constant can severely understate banks’ default risk in good times when asset values are high. Bank equity payoffs resemble a mezzanine claim rather than a call option. Bank equity return volatility is therefore much more sensitive to big negative shocks to asset values than in standard structural models.
(拙訳)
我々は、デフォルトリスクの構造モデルに銀行資産特有の特性を織り込んだ。対数正規分布する資産価値という通常の仮定は銀行にとって適切ではない。一般に銀行資産はリスクのある債権であり、債務者の資産に対する短期のプットオプションが内包されていることになるため、ペイオフは凹型となる。このことは、銀行のリスク動学とデフォルトへの距離の推計にとって重要な意味を持つ。ペイオフの非線形性により、銀行資産のボラティリティは債務者の資産価値が負のショックを受けた後に上昇する。そのため、資産のボラティリティが一定と仮定されている標準的な構造モデルは、資産価値の高い順境時のデフォルトリスクを大きく過小評価する可能性がある。銀行株式のペイオフはコールオプションよりはメザニン債に類似している。銀行株式のリターンのボラティリティは、従って、標準的な構造モデルにおけるのに比べて、資産価値への大きな負のショックに対する感応度がかなり高くなる。
以下はWPにおける債務者の資産を横軸に取った銀行の株式価値のグラフ(債務の満期前)。
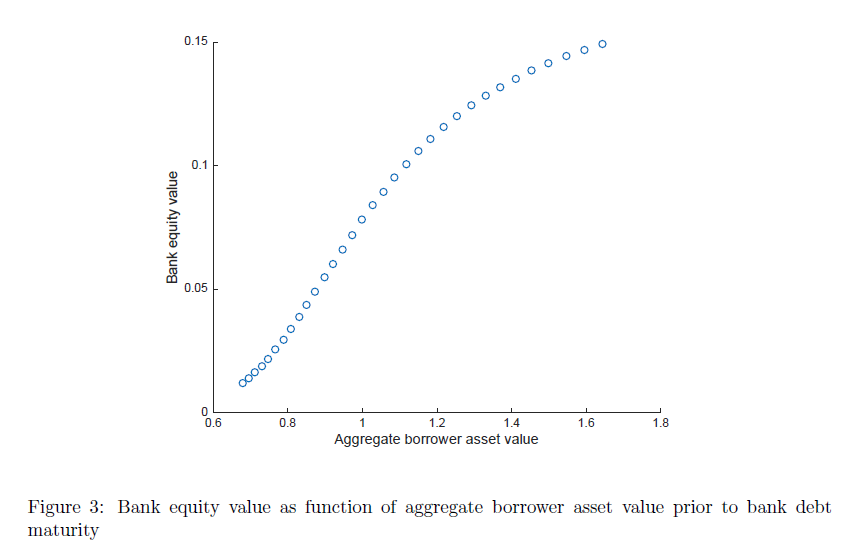
以下は銀行資産のボラティリティのグラフ(債務の満期前)。

以下は銀行資産、株式、債務のグラフ(債務の満期時)。
