ゼロと異なるp値の情報はすべて不完全

以前、サンプルサイズが大きくなると統計的有意性が高まるという話を紹介したが、カーネギーメロン大学の統計学者であるCosma Rohilla Shaliziが、自ブログ「Three-Toed Sloth」の表題のエントリ（原題は「Any P-Value Distinguishable from Zero is Insufficiently Informative」）で、p値についてその話を詳説している。（H/T Economist's View）。

そこでは5段階に分けた解説を行っているが、第一段階目では、「ゼロと異なる平均は任意の有意性を持つ（Any Non-Zero Mean Will Become Arbitrarily Significant）」という小題の下に、概ね以下のような解説を行っている。

μをゼロか否かを検定しようとしている平均パラメータ、 $\hat{\mu}$ をそのサンプル平均とした場合、検定量は $\frac{\hat{\mu}}{\hat{\sigma}/\sqrt{n}}$ となる。
ここでnが増加した時、中心極限定理により、
　　 $\sqrt{n}(\hat{\mu} - \mu) \rightarrow \mathcal{N}(0,\sigma^2)$
となることから、
　　 $\hat{\mu} \rightarrow \mu + \frac{\sigma}{\sqrt{n}}\mathcal{N}(0,1)$
となる。よって
　　 $\hat{\mu} = \mu + O(n^{-1/2})$
である。同様に、若干の計算から、
　　 $\hat{\sigma} = \sigma + O(n^{-1/2})$
が求まる。従って検定量は
　　 $\begin{eqnarray*}\frac{\hat{\mu}}{\hat{\sigma}/\sqrt{n}} & = & \sqrt{n}\frac{\hat{\mu}}{\hat{\sigma}}\\& = & \sqrt{n}\frac{\mu + O(n^{-1/2})}{\sigma + O(n^{-1/2})}\\& = & \sqrt{n}\left(\frac{\mu}{\sigma} + O(n^{-1/2})\right)\\& = & \sqrt{n}\frac{\mu}{\sigma} + O(1)\end{eqnarray*}$
となり、nが増大するに連れ、nの1/2乗の速さで、プラスもしくはマイナスの無限大に発散する。例外は、μが正確にゼロである場合のみである。一方、p値を計算する分布は標準正規分布（＝自由度が無限の場合のt分布）に収束するため、μ≠0の場合は、n→∞と共にp値は必ずゼロに近付く。

Shaliziはシミュレーションによるt検定量の推移を以下のグラフで示している。

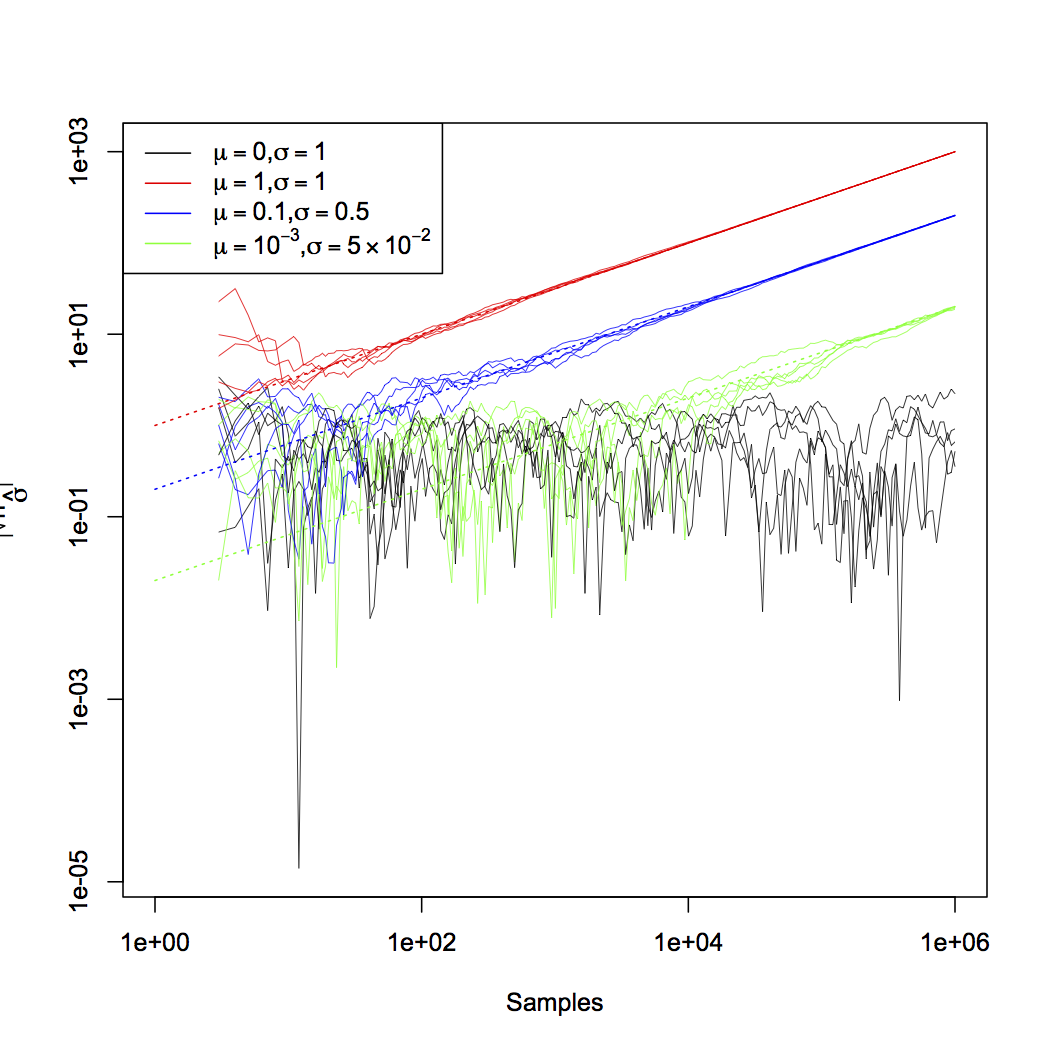
解説の第二段階目では、回帰係数について同様の解説を行っている。第三段階目では、平均や回帰係数といった特定のケースだけではなく、一致性を持つ仮説検定ではすべて、サンプルサイズを大きくすることにより検定力が任意の大きさにできることを示している。第四段階目では、平均のp値がゼロに近付く速さが指数関数的であることを示し、第五段階目ではそのことが一般的に成り立つことを示している。

以上を基にエントリの結論部でShaliziは、p値にあまり頼りすぎないように、と戒めている（…個人的には、そうした説教や精神論に走るのではなく、統計的検定量の利便性を維持しつつ問題を解決するような実務的な指針［例：冒頭でリンクしたエントリで紹介した、サンプルサイズの大きさに応じた棄却限界値を打ち出す、など］を統計学者にはお願いしたいような気もするが…。また、p値の解釈については第一線の統計学者の間でも未だに論争が繰り返されているので、それをさておいて非統計学者に対し上から目線で語られても、という気もする）。