と主張する論文が現下の統計学における最もホットなトピック/議論/展開である、としてFrancis Dieboldが紹介している。論文のタイトルはズバリ「統計的有意性の再定義(Redefine Statistical Significance)」で、Nature Human Behaviorに掲載予定との由。著者は総勢72名に及び、こちらのエントリで紹介したErnst Fehrも名を連ねているほか、日本人では今井耕介氏やShinichi Nakagawa氏の名前も見受けられる*1。
その1行要旨(One Sentence Summary)は概ね表題の通りで、原文は「We propose to change the default P-value threshold for statistical significance for claims of new discoveries from 0.05 to 0.005.」となっている。
以下は本文の冒頭部。
The lack of reproducibility of scientific studies has caused growing concern over the credibility of claims of new discoveries based on “statistically significant” findings. There has been much progress toward documenting and addressing several causes of this lack of reproducibility (e.g., multiple testing, P-hacking, publication bias, and underpowered studies). However, we believe that a leading cause of non-reproducibility has not yet been adequately addressed: Statistical standards of evidence for claiming new discoveries in many fields of science are simply too low. Associating “statistically significant” findings with P < 0.05 results in a high rate of false positives even in the absence of other experimental, procedural and reporting problems.
For fields where the threshold for defining statistical significance for new discoveries is 𝑃 < 0.05, we propose a change to 𝑃 < 0.005. This simple step would immediately improve the reproducibility of scientific research in many fields. Results that would currently be called “significant” but do not meet the new threshold should instead be called “suggestive.” While statisticians have known the relative weakness of using 𝑃 ≈ 0.05 as a threshold for discovery and the proposal to lower it to 0.005 is not new (1, 2), a critical mass of researchers now endorse this change.
We restrict our recommendation to claims of discovery of new effects. We do not address the appropriate threshold for confirmatory or contradictory replications of existing claims. We also do not advocate changes to discovery thresholds in fields that have already adopted more stringent standards (e.g., genomics and high-energy physics research; see Potential Objections below).
We also restrict our recommendation to studies that conduct null hypothesis significance tests. We have diverse views about how best to improve reproducibility, and many of us believe that other ways of summarizing the data, such as Bayes factors or other posterior summaries based on clearly articulated model assumptions, are preferable to P-values. However, changing the P-value threshold is simple, aligns with the training undertaken by many researchers, and might quickly achieve broad acceptance.
(拙訳)
科学的研究の再現性の欠如は、「統計的に有意な」発見に基づく新発見の主張の信頼性についての懸念を増大させている。この再現性の欠如をもたらす複数の原因(例:多重検定、pハッキング、出版バイアス、検定力の不足している研究)を明らかにし対処することについてはかなりの前進が見られた。しかし我々は、再現性の欠如の最大の原因は未だ適切に対処されていないと考える。それは、科学の多くの分野で、新発見を主張する際の実証結果に関する統計的基準がとにかくあまりにも低い、ということである。p値が0.05より低い結果を「統計的に有意な」発見とすることは、実験や手続きや報告についての他の問題が無い場合でも、偽陽性を高い割合でもたらすことになる。
新発見の統計的有意性の閾値がp<0.05と定義されている分野について、それをp<0.005に変更するよう我々は提言する。この単純な手続きは、多くの科学研究分野における再現性を直ちに改善するであろう。現在「有意」と呼ばれているが新たな閾値を満たさない結果は、「示唆的」と呼ぶものとする。統計学者はp<0.05を発見の閾値に使うことの相対的な弱点を以前から知っており、それを0.005に低めるという提言は新しいものではないが(1*2、2*3)、今やこの変更を支持する研究者は臨界点に達した。
我々は提言を、新たな効果の発見の主張に限定する。既存の主張を確認もしくは覆す再現結果についての適切な閾値については対象としない。また、より厳格な基準を既に採用している分野(例えばゲノミクスや高エネルギー物理学研究など。後述の「あり得る反論」の項を参照)の発見の閾値の変更を提唱するものでもない。
我々はまた、帰無仮説の有意性検定を行う研究に提言を限定する。再現性を改善する最善の方法については我々の中でも意見が分かれており、多くの者は、データを要約する別の方法がp値より好ましい、と考えている。例えば、明確に記述されたモデルの仮定に基づくベイズファクターなどの事後の要約統計量である。しかしながら、p値の閾値を変えるのは単純であり、多くの研究者が受けてきた訓練の延長線上にあり、すぐに広く受け入れられる可能性がある。
論文では、0.5%という閾値を選択した理由として以下の2つを挙げている。
- 両側検定のp値=0.005は、代替仮説H1を選好するベイズファクターにしておよそ14〜26に相当するが、ベイズファクターの通常の分類によれば、これは「実質的(substantial)」ないし「強力(strong)」な実証結果に相当する(cf. ここ)。
- 偽陽性率が合理的な範囲まで下がる。
2番目のポイントについて論文では、閾値や事前確率の変化に伴う偽陽性率の変化を図示しているが、それは、小生が7年前のこのエントリで描画したものに似ている。そこで、小生が当時Jacob Cohen論文の統合失調症の診断の例から持ってきた記法と今回の論文の記号を組み合わせる形でその例示を表現すると、以下のようになる。
- H0=帰無仮説(病気は無い)
- H1=代替仮説(病気は有る)
- φ=P(H0)、1−φ=P(H1)
- 無病正診率 P(正常|H0) =1−α
- 有病正診率 P(疾病|H1) =1−β(誤った帰無仮説を棄却する検定力)
ここで
- D=病気があると診断された結果(データ)
とすると、ベイズの定理より、
P(H0|D)
= {P(H0)×P(誤診|H0)} ÷ {P(H0)×P(誤診|H0)+P(H1)×P(正診|H1)}
即ち
偽陽性率(診断を受けた人が病気があるという結果が出たが、それが間違いである確率)
= {φ×α} ÷ {φ×α + (1−φ)×(1−β)}
となる。
7年前のエントリを書いた時には、小生は偽陽性率とφを変化させて、P(H0|D)(=偽陽性率)とP(D|H0)(=P(誤診|H0)=病気が無い人を病気があると診断する確率)がどの程度乖離するかを見たのだが*4、今回の論文では、φとαと1−βを変化させて、偽陽性率がどのように変化するかを見ている。そのうちのαについては、0.05もしくは0.005として、有意水準を下げることによって偽陽性率がどの程度下がるかを見ている。
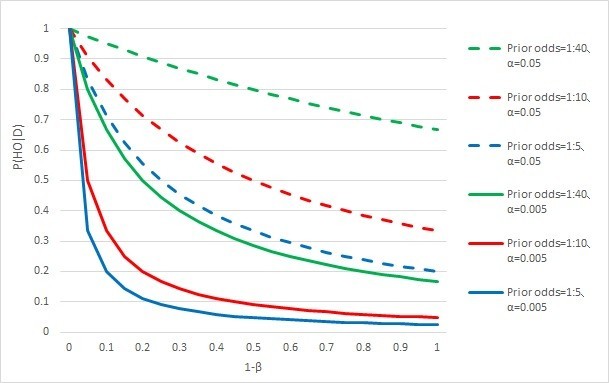
論文の図をExcelで再現すると以下の通りとなる(ここでPrior odds=(1−φ)/φ)。
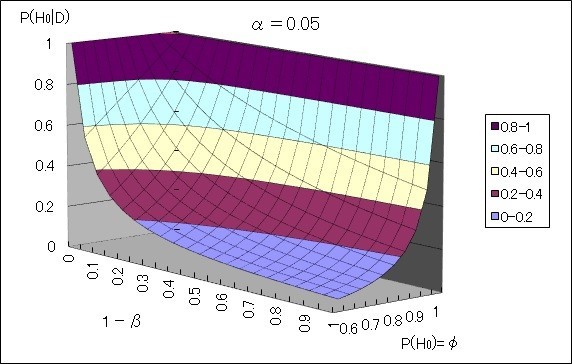
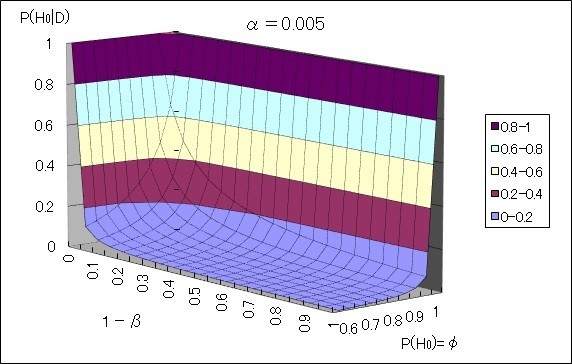
また、7年前のエントリと同様に3Dグラフにしてみると次のようになる。
いずれの図からも、確かにαを5%から0.5%にすることによって偽陽性率が低下することが分かる。
なお、論文がαを0.005にする1番目のポイントの中で重視する要因として挙げたベイズファクターは、
P(H1|D) ÷ P(H0|D) = ベイズファクター × P(H1) ÷ P(H0)
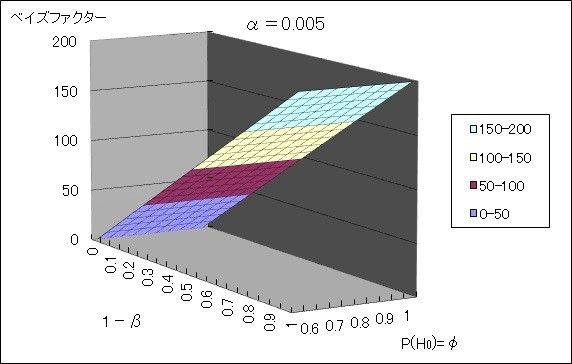
として定義される(P(H1) ÷ P(H0)=Prior odds)。上の3D図をベイズファクターについて描画すると以下のようになる。

以前小生は、「統計的検定量の利便性を維持しつつ問題を解決するような実務的な指針を統計学者にはお願いしたいような気もする」と書いたことがあったが、期せずしてこの論文は小生のその願いへの回答になっているように思われる。ただ、Dieboldはこの論文の提言に対して冷淡であり、5%にしろ0.5%にしろp値の閾値という概念そのものの存在意義に疑念を呈している。