SIRモデルでの実効再生産数の極限は？

医療 統計

以下のツイートを目にして、実際の測定値はともかく、感染モデル上は感染が収まった時に実効再生産数はどうなるのか、という疑問を抱いた。


SIRモデルについては、RIETIの関沢洋一氏がExcel上で仮想的な数字で計算できる方法を公開している。また、基本再生産数を含めたSIRモデルの簡単な解説としてはここで読める鈴木＝西浦論文がある*1。関沢氏は感染率をb、除去率をcという記号で表しているので、基本再生産数R0はb/cとなる。b=1.5、c=0.5という関沢氏の数字を使えば、R0=3である。また、実効再生産数Rtは、同様に関沢氏の表記を使えば、R0×S(t)/S(0)で計算できる。

以下は、関沢氏のSIRモデルの図を再現したS（無免疫者数）、I（当該時点の感染者数）、R（感染経験者数）の推移グラフと、その場合の実効再生産数の推移グラフである。
f:id:himaginary:20211003150341p:plain
f:id:himaginary:20211003150710p:plain
これから分かるように、実効再生産数は最終的にはゼロに近い値（計算上は0.0747）に落ち着く。

ただ、実際にはSIRモデルを当てはめて実効再生産数を算出するのは難しいので、感染者数の伸び率から実効再生産数を計算するのが普通である。そうした近似の手法については、例えばこの論文*2で以下の近似式が示されている。
　R = 1 + r×T
ここでrは指数関数に当てはめた人口当たり新規感染者の増加率、Tは平均世代間隔（1次感染から2次感染までの時間間隔）である。
SIRモデルではTは除去率の逆数となるので*3、上記モデルではT=1/c（c=0.5ならば2）となる。そこで、rをIの単純な伸び率として1+r/cを計算し、元の実効再生産数と比較すると以下のようになる。
f:id:himaginary:20211003154157p:plain
感染拡大のピーク期前後を除き、良い近似になっていることが分かる*4。

なお、この実効再生産数の近似式で注意すべきは、モデル上はIが1以下の極めて小さな値になった後も同率で減少していく形になっているので近似が最後まで成立しているが、実際の感染者数は当然ながらゼロ以上の整数なので、実測値ではそうはならない点である。r=0に収束すれば、冒頭でリンクしたツイートが指摘するように、上記の近似式は1となる。一方、rの最小値は正の値から0に変化する-1なので、感染者数がゼロとなった期には近似式は1-1/c（c=0.5ならば-1）となる。また、感染者数がゼロから再びプラスになればrは無限大になるので、近似式も無限大となってしまう。

*1:なお、同論文では、実効再生産数という言葉を、対策によって基本再生産数から低下する、という文脈においてのみ使用しているが、論文の(2)式の右辺の係数が、SIRモデルによる実効再生産数の定義になっている（cf. 基本再生産数 - Wikipedia。ちなみに後述のDas論文でも、実効再生産数について「expressed mathematically as R=R0 ∗(S/N), where S = number of susceptible and N = total population」と説明している）。

*2:Das A. (2020). An approximation-based approach for periodic estimation of effective reproduction number: a tool for decision-making in the context of coronavirus disease 2019 (COVID-19) outbreak. Public health, 185, 199–201. https://doi.org/10.1016/j.puhe.2020.06.047

*3:Das論文で参照されているこちらの論文（Wallinga, J., & Lipsitch, M. (2007). How generation intervals shape the relationship between growth rates and reproductive numbers. Proceedings. Biological sciences, 274(1609), 599–604. https://doi.org/10.1098/rspb.2006.3754）参照。

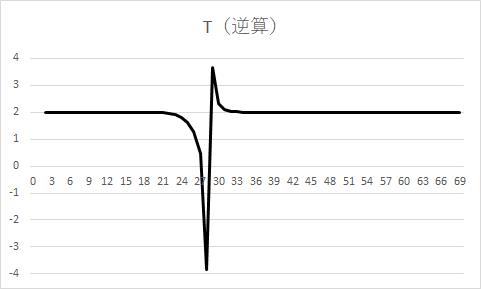
*4:ちなみに近似式が常に成立しているとしてTを逆算すると以下のようになる。感染者数が増え始めると実際の実効再生産数の低下に追いつくためにTが低下し、ピークを付けた期にはマイナス3.84に落ち込む。次の期にはrがマイナスに転じたことを受けてTは3.68に跳ね上がり、その後は再び2に収束していく。
f:id:himaginary:20211003161207p:plain