というNBER論文が上がっている(ungated版)。原題は「The Micro and Macro Productivity of Nations」で、著者はStephen Ayerst(IMF)、Duc M. Nguyen(トロント大)、Diego Restuccia(同)。
以下はその要旨。
We examine aggregate productivity differences across nations using cross-country firm-level data and a quantitative model of production heterogeneity with distortions featuring operation decisions (selection) and productivity-enhancing investments (technology). Empirically, less developed countries feature higher distortions and larger dispersion in firm-level productivity, mostly resulting from the higher prevalence of unproductive firms. Quantitatively, measured cross-country differences in the elasticity of distortions with respect to firm productivity generate the bulk of empirical patterns and over two-thirds of cross-country labor productivity differences. Both selection and technology channels are important. Variation in static misallocation also plays an important role, albeit smaller.
(拙訳)
我々は、各国の企業レベルのデータと、事業の決定(選択)と生産性増強的な投資(技術)を特徴とする歪みのある生産性の不均一性の定量モデルを用いて、国同士のマクロの生産性の違いを調べた。実証的には、発展が遅れた国では、非生産的な企業がより一般的であることを主因として、企業レベルの生産性の歪みと分散が大きくなる。定量的には、各国の測定された歪みの企業の生産性に対する弾力性の違いが、実証パターンの大部分と、各国の労働生産性の違いの2/3以上をもたらす。選択と技術の両経路が重要である。静的な誤配分の違いも、それよりは小さいが、重要な役割を演じる。
以下は論文の図1。フランスの生産性の分散はハンガリーやスペインよりも小さく、各国の最も生産的な企業の差に比べ、分布の下端の企業の差が大きい。ハンガリーのおよそ半分の企業はフランスの下位1%の企業よりもTFPが低い半面、フランスの1割強の企業のTFPはハンガリーの上位1%を上回っている。

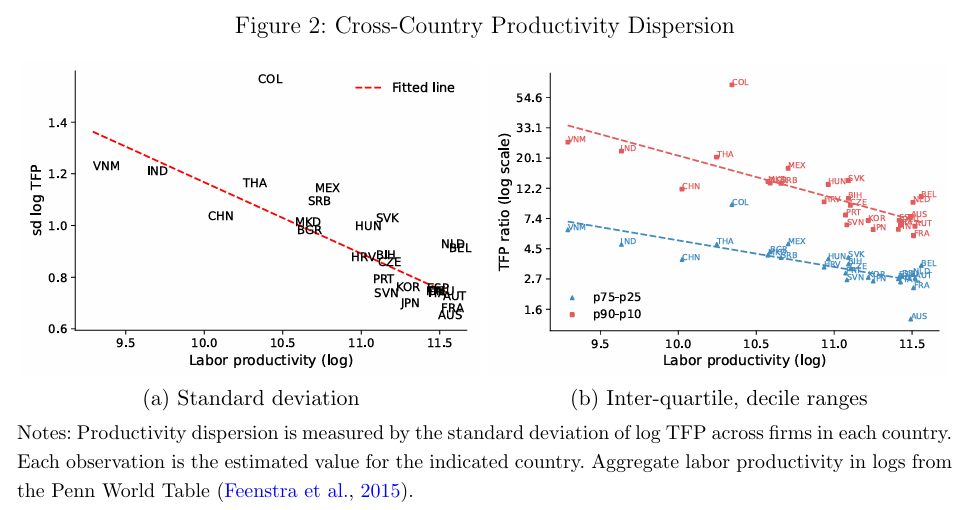
以下は、企業のTFPの分散と各国の労働生産性の関係を示した図。日本も概ね傾向線に沿っている。
モデルでは企業の生産は以下のように定式化されている。
yi = vizi1−γniγ
ここでniは労働力、zi1−γはTFPの恒常的要因、viは一時的要因、γ ∈ (0,1)である。
歪みは収益に対する比例税として以下のように定式化されている。
(1 − τi) = (zi−ρϵi)1−γ
ここでτiが比例税、ϵiはランダム項、ρがTFPに対する歪みの弾力性となる。
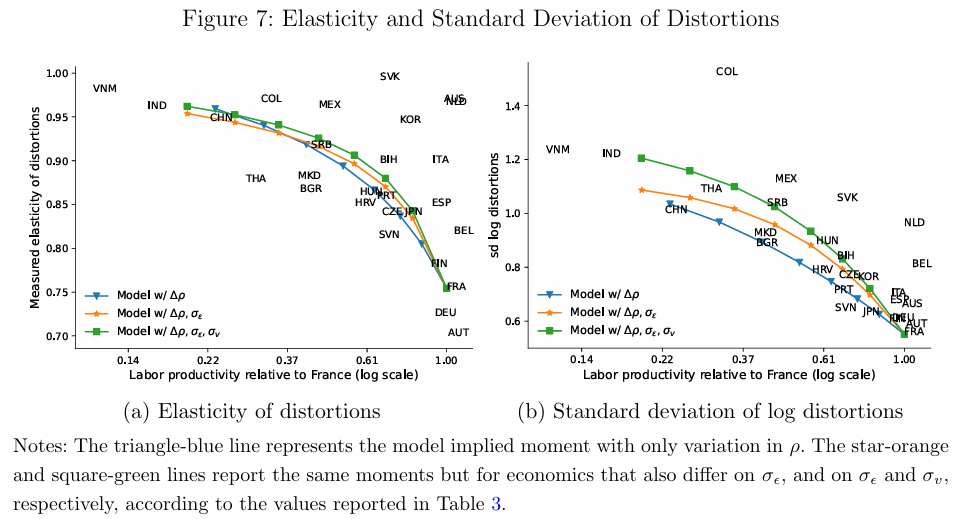
以下は、弾力性とその分散についてモデルの当てはまりを示した図。日本はほぼモデルの予測通りとなっている。