ゲーム理論入門／（５）チキンゲームのナッシュ均衡

チキンゲームのナッシュ均衡

		少年２
		逃げない	逃げる
少年１	逃げない	死(-100)	英雄(10)
	逃げる	チキン(-10)	チキン(-5)

＜純粋戦略でのナッシュ均衡＞

このゲームのナッシュ均衡は純粋戦略では（逃げる、逃げない）（逃げない、逃げる）の2通り。

∵）

相手が逃げるのを所与とすれば、自分は逃げないのが最適反応戦略

相手が逃げないのを所与とすれば、自分は逃げるのが最適反応戦略

→定義により、片方が逃げて片方が逃げないのがナッシュ均衡となる

＜混合戦略でのナッシュ均衡＞

少年２が逃げる確率をp₂とすれば、少年１が確率p₁で逃げ、確率1-p₁で逃げないという混合戦略を取れば、その利得は
　-5p₁p₂ -100(1-p₁)(1-p₂) -10p₁(1-p₂) +10(1-p₁)p₂
= -105p₁p₂ +90p₁ +110p₂ -100
= p₁(-105p₂ +90) +110p₂ -100
となる。

従って、
p₂ > 6/7 ならばp₁ =0（逃げない）
p₂ < 6/7 ならばp₁ =1（逃げる）
が少年１の最適反応戦略となる。（p₂ =6/7 の場合、p₁は不定）

少年２についても同様。

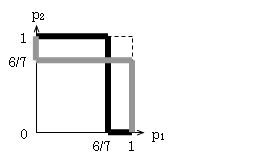
従って、（p₁ =0、p₂ =1）（p₁ =1、p₂ =0）のほかに、（p₁ =6/7、p₂ =6/7）、すなわち、両者が共に確率6/7で逃げる、という混合戦略の組み合わせもナッシュ均衡となる（下図参照）。
（そのときの両者の利得はそれぞれ -40/7）